Turing machine with a tape 60 million cells in length

[eah]

How? Well, we can’t build a tape that is that long.

Here’s the idea: don’t build the tape. Let the game generate it for us. Set the world generator to superflat and then the game will give us a “tape” that extends to the world border in each direction, a length of a little less than 60 million blocks. The tape is just a single horizontal strip in the top layer of solid blocks. A 0 symbol can be the presence of a block in the strip and a 1 symbol can be absence. Notice that not yet visited portions of the tape are filled with 0s with the help of the superflat world generator.

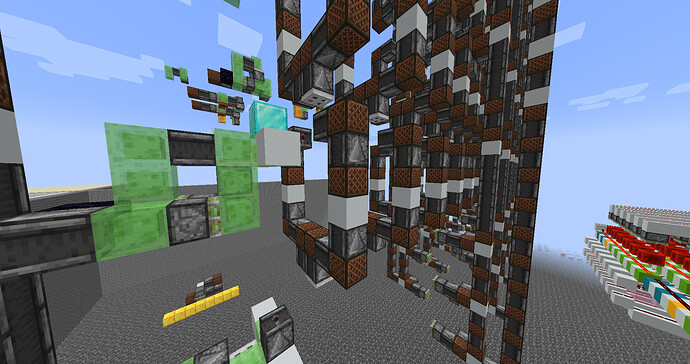
In order to be a Turing machine, it also needs a read/write head that can move in each direction along the tape, a way to remember the current state, a table of transitions, and the logic that fits all this together. Notice that the tape, as defined, is stationary, and so the head will need to be the thing that moves (in contrast to the natural way TMs are implemented in MC, using piston tapes). And this leads us to… flying machines.

Can we use flying machines to accomplish this feat? It seems so. At one end of the tape, fix a stationary structure, a ROM for the table of instructions. Next, we need a movable structure, perhaps just a single block along the tape that indicates the current position of the head. Then we need a flying machine that moves between the ROM and the head position indicator, which can read the symbol at the head, change the symbol, and move the head indicator in either direction. The head position indicator causes the flying machine to stop, perform an action, and then reverse direction back to the ROM. Changing the symbol at the head can be accomplished with a downward-facing sticky piston that lowers or raises the block at the head. Reading a symbol and moving the head indicator can be done, but are too complicated to describe briefly in words.

So, relatively easily we have a computer with 7.5MB of memory buildable in superflat using items obtainable in survival. And with cobblestone generators it can be built in a regular survival world.

But this is kind of unimpressive. And our machine has a flaw; the speed of the machine is proportional to the head’s distance from one end of the tape. Can we do better?

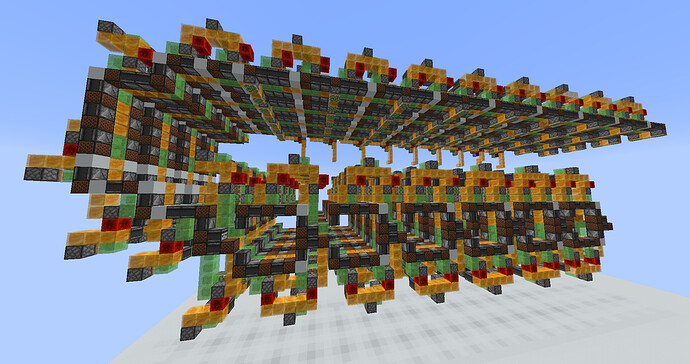
Maybe. But it would mean the entire ROM would need to move with the head indicator. And so static redstone like redstone dust, torches, and repeaters would not be allowed. The ROM would be composed of individual moving parts (pistons, observers, slime blocks, etc.) in order to do logic and the ROM collectively would itself be a moving part. It would all need to move left and right along the tape while preserving its internal structure. This proves difficult because the individual parts making up the ROM, when moved, tend to activate nearby parts as that’s what they’re made to do.

Note that the ROM can’t be built out of the typical piston-based logic gates since the NOT gate will have at least one piston extended (either at the input or output) which is an immovable block. So, some clever solution is needed.

Perhaps logic gates can be abandoned. Imagine instead that there is a flying machine that carries with it the current state encoded as a binary number and it scans along some structures looking for a matching state, at which location there is data on what to do next. Unfortunately, I only have vague descriptions and ideas, so sorry if this doesn’t make sense.

Anyway…

Reasons why this would be awesome:

• It’s a Turing machine, the simplest and most fundamental of computers, with a very long tape.
• It may be the first computer in MC with 7.5MB of memory buildable using items obtainable in survival.
• There’s no static redstone. The entire structure moves left and right according to the rules of a program (any program!), and the structure that is moving contains the rules of the program that describes its movement. It feels satisfyingly self-referential. It’s a fully programmable flying machine!

[eah]

I went ahead and tried to build this. So far I’ve built flying machine memory which a player can operate. You can increment and decrement an address pointer, and read and write at the address at the granularity of individual bits. The time to read/write at address n is O(n) and the time to seek the address pointer a distance of n is O(n^2). Pasted into a superflat world, it can store up to ~7.5 Megabytes. A read/write of a single bit can take up to around 2 years to complete and a seek can take up to ~114 million years. You can try it out at /warp flying_machine_memory.

[eah]

I completed the building of a Turing machine with 2 symbols, 32 states, and with a tape “infinite” in one direction.

Here it is computing n mod 3 for a given n (in this case 13). The number is encoded on the tape made up of gold blocks, with a single up block representing a 0 and 2 up blocks representing a 1, separated by down blocks. From the perspective in the video, the number is written backwards with the least significant bit appearing on the left. The 5 redstone lamps in the distance on the left show the current state and can also display a number of my choosing when it halts. In this case, I have it show the result, n mod 3. It takes around 3 minutes for a 4-bit number.

Here it is deciding whether a given input is a string of balanced parenthesis. An opening parenthesis is a single up block and a closing parenthesis is 2 consecutive down blocks. In the video, it’s processing the string “(()())” and takes about 45 minutes. It returns 0 if the input is balanced and nonzero if not. The algorithm works by keeping a counter initialized to 0, and scanning the string from left to right, incrementing if you see a opening parenthesis, decrement if you see a closing parenthesis, and if at any point you try to decrement when the counter is 0, it’s not balanced, and if you reach the end when the counter is nonzero, it’s not balanced. Otherwise, the input is balanced. Of course, since the input can be arbitrary long and a Turing machine has only finite memory, it will need to store the counter (which I do in unary) at the end of the tape (the sponge blocks), and remember its scanning place on the input.

There are some other programs I could write to demonstrate its power, but it turns out 2 symbols and 32 states is quite limiting, making even something as simple as computing a number’s square a challenge. However, it wouldn’t be too hard to extend it with more symbols or states. So I really reached my goal and moved on.

In the videos above, you’ll notice a moving component made of honey blocks which can move left or right 1 block. This is the so-called read/write head of the Turing machine whose position determines which symbol on the tape the machine reads or writes to next. You’ll also notice the time that the machine takes to make progress is linear with the head’s distance to the right. I want this time to not depend upon the head’s position.

So I’ve built a structure that might help with that.

On its own, this is an esoteric implementation of a fixed function from 2^7 to 2^9. In digital circuit parlance, I think this is called a ROM of 128 9-bit words. The idea of building it this way with observers and note blocks is so that the entire structure (hopefully) can be moved left or right with pistons while preserving the structure, enabling the Turing machine’s entire action table (which is really just a ROM) to move in sync with the TM’s read/write head. To be most useful, the ROM should be larger (say 2^11 to 2^13). I chose this small ROM because I wanted to start small and because I was inspired by this 2011 video of a universal TM in MC which uses this simple universal TM designed for the game of life. It has a simple, human-readable encoding and requires only 8 symbols and 13 states. So that’s 3 bits for the symbol, 4 bits for the state (so 7 bits input), and an extra 2 bits for the direction to move (or whether to halt) at the output. It will need 82 state-symbol pairs after pruning unnecessary pairs, so the ROM will need to be 4*82=246 blocks long.

This could help with moving the ROM. Since the ROM may be so large that it extends beyond the player’s render distance, the player will need to ride in a flying machine that extends individual sections of the ROM as it passes by. This is what this does. The position of an observer on the flying machine determines the direction the pieces are shifted.

These are so-called pushing and pulling flying machine extensions that basically enable getting past the 12-block piston limit.

The ROM up close. 7 flying machines carry 7 input bits (determined by the position of the diamond blocks and 1 observer), scanning along the ROM structure until it finds a match, which causes the inputs to change, becoming the outputs, and the flying machines to move back to start.

[eah]

Movable programmable read-only memory

[eah]

Here’s a video of the ROM. It’s simultaneously queried and moved. The first time it moves 1 block west and the second time it moves 1 block east. A set of 7 flying machines carry the input bits through the ROM and another set of 9 return with the result.

[StackDoubleFlow]

Sounds like chunkloading hell lol

[eah]

It will be very slow. But I did try a tick speed mod on what I have built so far and it doesn’t handle it well, I think due to so many updates sent to the client in a short time frame. It can’t keep up with the server.

[eah]

In case I completely lose interest in this project or never finish it, I’m going to summarize the goal here and describe what I have so far so that someone might pick it up.

The goal is basically a flying machine computer. We can have the machine be of a relatively small finite size and have it use the top layer of movable blocks of a superflat world for memory. This top layer can be moved up or down with sticky pistons. There are methods of “reading” from this memory as well. The nice thing about this is the available memory is virtually unlimited. Despite this, you could, hypothetically, build the machine in survival since the machine is of a finite size and you get all of the memory and space to move around for free by the superflat world generator.

This is actually fairly easy to build using some static (immovable) redstone. I’ve built it. You can find it on my plot.

But the goal is to use no static redstone and have the entire computer move throughout the world to wherever it needs to read/write memory. The player can ride along with the machine to keep it in a loaded region.

This sounds complicated and it’s not clear where to start.

So let’s simplify it. CPUs are typically fairly complicated. Even the simple ones we build in minecraft. We need something even simpler. Perhaps something out of the mathematician’s playbook. A Turing machine. They’re terribly slow, impractical computers, but they’re incredibly simple. Some other possibilities are an esoteric programming or some Turing machine equivalents. Though, I’d argue that Turing machines, with the way they are imagined as real machines with moving parts scanning along an unlimited memory tape reading and writing symbols, are a perfect match to the flying machine we are imagining moves throughout the virtually unlimited minecraft world reading and writing bits.

My progress so far I think can best be described as being in a late prototyping phase.

One component that a Turing machine needs is the programmable fixed action table. It must be movable in both directions along at least 1 axis. This will be the largest component of the machine and it will be made up of a modular component that can be stacked, so I started on this first. I have managed to build something that fits this description. It’s basically a ROM that can be moved by 1 block in either direction along 1 axis. Bits are carried into the structure by a set of flying machines and some other bits are carried out. Whenever it’s queried, you have a choice of which direction to move the structure.

I also have some movable components that can read/write from the tape.

More or less what is needed now is to figure out how to wire it all together so that it runs in a read-fetch-write-move loop. This is not as easy as it sounds because… well, it’s flying machines. Everything needs to be triggered with the right timing so that it arrives at the right moment and right place, etc. It’s not as simple as adding a repeater for a delay. You can’t immediately look at it and know after how many ticks a flying machine will arrive.